[Uma economia de mercado é um sistema inerentemente dinâmico, com atores cuja agência perturba continuamente qualquer possibilidade de se alcançar um equilíbrio mecânico como o esperado pelas teorias herdadas do século XIX, no qual a configuração do sistema permanece estática até que seja aplicada alguma força externa. Em uma modelagem probabilística, encontramos um tipo diferente de equilíbrio: um sistema pode estar em equilíbrio estatístico, mesmo enquanto sua configuração muda continuamente. É a distribuição das probabilidades entre as possíveis configurações do sistema o que permanece constante ao longo do tempo. No entanto, um equilíbrio desse tipo pode ferir profundamente a visão do capitalismo como um sistema ideal. ]
por Ian Wright, em “Classical Econophysics” (“Econofísica Clássica”), 2009
[Nota do Minhocário: O texto abaixo é a tradução do capítulo 7, “The probabilistic approach to economic variables” (“A Abordagem Probabilística Para as Variáveis Econômicas”), escrito por Ian P. Wright para o livro “Classical Econophysics” (“Econofísica Clássica”), publicado em 2009 por W. Paul Cockshott, Allin Cottrell, Gregory J. Michaelson, Ian P. Wright e Victor M. Yakovenko. Há algumas referências a questões discutidas em outros capítulos do livro, e sempre deixei indicado esse conteúdo.
O artigo envolve alguns conceitos e equações de Física e Matemática que podem assustar um pouco leitores menos familiarizados, mas mesmo que não se domine esses conceitos, vale a pena acompanhar (ainda que um pouco superficialmente) o desenvolvimento das ideias, assumindo como dadas as equações utilizadas (ou mesmo às ignorando) – embora, evidentemente, esse conhecimento possibilite uma melhor compreensão dos argumentos apresentados pelo autor. Tentei deixar pelo menos o link para o termo na Wikipédia na primeira ocorrência da maioria dessas situações, e, em alguns casos, mantenho entre colchetes meus comentários, a fim de tentar facilitar pelo menos a compreensão básica dos símbolos e equações apresentados.]
- Modelos probabilísticos
- 1. Uma economia de trocas simples
- 2. O conceito de equilíbrio estatístico
- 3. A distribuição de máxima entropia
- 4. Agentes aleatórios versus agentes racionais
- Anexo 1 – A distribuição de Boltzmann-Gibbs
Neste artigo [1], discutiremos as diferenças entre os conceitos de equilíbrio estatístico e equilíbrio mecânico em sistemas com grandes níveis de liberdade [ou seja, com grande número de elementos e de possibilidades de ações para cada um deles].
Modelos Probabilísticos
Uma vez que conheçamos os possíveis resultados de uma situação, é natural considerar a probabilidade de ocorrência de cada um desses resultados. A probabilidade de um evento é um número no intervalo entre 0 e 1, onde 0 representa um evento impossível e 1 um evento cuja ocorrência é certa.
Por exemplo, se lançarmos uma moeda um grande número de vezes, logo descobrimos que cerca da metade dos resultados são cara e metade coroa. Portanto, embora não possamos prever o resultado de um lançamento específico, podemos dizer que é igualmente provável que o resultado seja cara ou coroa – ou, mais precisamente, que a probabilidade de dar cara ou de dar coroa é metade: P(X = cara) = P(X = coroa) = 1/2, onde X é o resultado do lançamento da moeda.
Saber que P(X = cara) = 1/2 significa que cerca de metade das vezes o lançamento da moeda vai acabar dando em cara. De fato, essa é uma previsão probabilística da frequência para um resultado específico – ela não prevê o que de fato vai ocorrer, mas o que provavelmente vai ocorrer, dado o conhecimento dos possíveis resultados. Embora seja mais fraca que uma previsão determinística, uma previsão probabilística ainda é muito útil para se atuar no mundo. Por exemplo, saber que uma área possui uma alta probabilidade de atividades tectônicas nos diz que devemos construir casas robustas, mesmo que não saibamos exatamente quando um terremoto ocorrerá.
A teoria da probabilidade é uma ferramenta apropriada para situações em que simplesmente não conhecemos toda a gama de mecanismos causais que determinam o resultado de uma situação, ou para casos em que achamos que sabemos o que determina o resultado, mas onde na prática é difícil de usar nossas teorias para fazer previsões robustas. Nesses casos, desistimos da ideia de prever os resultados reais, mas, ao invés disso, prevemos o que provavelmente ocorrerá, considerando os possíveis resultados conhecidos. Em vez de usarmos um modelo determinístico para prever o valor de uma variável x – como prever se x será igual a cara ou coroa – usamos um modelo probabilístico para prever a distribuição de uma variável aleatória x, como na previsão de que P(X = cara) = 1/2 e P(X = coroa) = 1/2, o que equivale a afirmar que a distribuição de X é uniforme, ou seja, que todos os resultados têm uma probabilidade igual de ocorrência.
Considere as decisões de compra de todas as pessoas nos EUA durante um mês. Há uma enorme variedade de razões pelas quais certas mercadorias são vendidas em determinadas quantidades por determinados preços. Alguns produtos são comprados regularmente em quantidades estáveis, como itens de necessidade básica como gás ou água; outros são efêmeros e suas vendas dependem de modas passageiras, como o mercado de brinquedos para crianças. O clima pode afetar as vendas. As pessoas são muito diferentes e possuem objetivos e gostos diferentes. Alguns produtos se desgastam periodicamente e podem precisar ser substituídos. Em suma, existem quase tantas razões para eventos de troca quanto os próprios eventos.
A variabilidade e a contingência que necessariamente ocorrem quando seres humanos complexos e inteligentes interagem competitivamente entre si implica que é impraticável tentar modelar detalhadamente as trocas de mercado. Embora seja possível modelar e prever o comportamento humano em ambientes experimentais controlados que restringem o espaço de possíveis ações, ou em situações em que convenções ou regras desempenham um papel importante, não é possível modelar a criatividade cotidiana de participantes do mercado que buscam satisfazer seus objetivos em ambientes econômicos abertos e mutuamente constituídos. É evidente que, tirando casos especiais, prever o preço real de um bem em um determinado dia ou prever a demanda por um tipo de mercadoria recém-inventada, é uma causa perdida. Os preços e as mercadorias estão sempre mudando. Uma economia de mercado representa, portanto, um candidato ideal para uma modelagem probabilística.
1 Uma economia de trocas simples
Recentemente, físicos têm voltado sua atenção para os fenômenos econômicos, criando um novo campo chamado Econofísica. As abordagens econofísicas para os problemas econômicos tradicionais são essencialmente probabilísticas por natureza. Podemos ilustrar essa abordagem examinando um modelo muito simples de uma economia de mercado desenvolvido pelos físicos Dragulescu e Yakovenko (2000).
Imagine uma economia simples composta por N pessoas, que chamaremos de atores. Cada ator possui uma quantia em dinheiro m, que, em nome da concretude, vamos assumir que seja denominada em dólares. A quantidade total de dinheiro na economia, que é simplesmente a soma de todos os valores individuais de dinheiro mantidos por cada ator, é uma constante fixa M.
Em uma economia de mercado, as pessoas trocam bens e serviços por quantias em dinheiro. No entanto, vamos abstrair completamente a natureza desses bens e serviços, o tempo que levam para serem produzidos e concluídos e quem produz o que e quando. Também não vamos considerar as instituições – portanto, empresas, bancos e operações econômicas estatais estão fora do quadro. Em vez disso, nos focaremos em uma característica essencial de uma economia monetária dinâmica – o fato de que o dinheiro é trocado continuamente entre os atores em diferentes quantidades, mas quase sempre é conservado. [2] Não tentaremos modelar deterministicamente todas as razões locais pelas quais determinados atores trocam quantias específicas de dinheiro em momentos específicos no tempo, mas, ao invés disso, vamos assumir que toda essa contingência possa ser modelada como um ruído aleatório. Dadas essas robustas abstrações, um único procedimento pode conduzir a dinâmica desse modelo simples:
- (1) Escolher aleatoriamente dois atores, um comprador e um vendedor, de maneira que cada ator tenha a mesma chance de ser selecionado.
- (2) Escolher aleatoriamente um preço p para a transação, dentro do intervalo de 0 até a quantia de dinheiro mantida pelo comprador.
- (3) Reduzir o dinheiro mantido pelo comprador em p e entregar essa quantia ao vendedor.
A mudança econômica é simulada pela aplicação repetida dessa regra à população de atores. A regra transfere quantias aleatórias de dinheiro entre indivíduos selecionados aleatoriamente – e é só isso. Podemos chamar esse modelo de economia simples. Como mencionado, é um modelo muito simples – tão simples que talvez seja difícil acreditar que ele possa ter muito a contribuir para a nossa compreensão. Contudo, de fato, ele é capaz de replicar uma das regularidades empíricas mais duradouras e características das economias de mercado.
Os números de atores que possuem $0, $1,. . . , $M nos bolsos podem ser contados. Podemos considerar cada quantia em dólares como um “recipiente”, e qualquer ator específico, em um determinado momento, estará em um desses compartimentos, dependendo de quantos dólares possuir. Por exemplo, se inicializarmos o modelo para que cada ator possua a mesma quantidade de dinheiro (M/N dólares) e então medirmos o tamanho de cada um desses recipientes em dólares, descobriremos que a distribuição do dinheiro estará degenerada: Todos os compartimentos estarão vazios, exceto o compartimento de M/N, que terá o tamanho N. Essa distribuição é chamada de degenerada porque existe apenas uma possibilidade.
No entanto, se nosso procedimento de troca for aplicado repetidamente, a distribuição começará a divergir de seu estado degenerado, à medida que o dinheiro seja trocado em quantidades desiguais entre os atores. Alguns atores terão sorte e desfrutarão de uma sequência de negociações vantajosas, obtendo grande riqueza, enquanto outros podem gastar o dinheiro repetidamente e receber muito pouco em troca. Se esse processo continua, a economia se estabiliza em uma distribuição de Boltzmann–Gibbs, [seguindo a equação [10]]:
A distribuição do dinheiro fica altamente desigual. A maioria dos atores fica com muito pouco dinheiro, enquanto exponencialmente poucos ficam com muito dinheiro – de fato, um número muito pequeno de indivíduos acaba possuindo quantias relativamente enormes de dinheiro. [3]
Notavelmente, a distribuição exponencial da riqueza é encontrada em dados reais de economias reais. Há alguma divergência em relação a uma distribuição exponencial para algo entre 5% e 10% de indivíduos mais ricos, mas uma distribuição exponencial da riqueza descreve com precisão a grande maioria da população (Dragulescu, 2002; Dragulescu e Yakovenko, 2002), para qualquer país capitalista avançado que for considerado. [4] Essa distribuição também se mantém estável por longos períodos de tempo. Embora a riqueza média possa mudar de um ano para o outro, a forma funcional geral da distribuição da riqueza permanece exponencial. Podemos concluir que o modelo probabilístico simples, apesar de (ou será que graças a isso?) seu alto nível de abstração e simplicidade, foi capaz de replicar uma característica importante das economias capitalistas modernas.
Pode-se pensar que as diferenças de riqueza tenham surgido em parte por uma combinação de acidentes no nascimento e em parte por virtudes pessoais. Podemos aceitar que a escolha de nossos pais seja fortuita, mas certamente o esforço, a diligência e a inteligência explicariam o resto, não?
Bem, em algumas sociedades, isso pode ser verdade, mas Yakovenko e Dragulescu parecem estar nos dizendo que em uma sociedade monetária, dominada pela venda de bens e serviços em troca de dinheiro, não seria preciso procurar além da operação cega da sorte para explicar a distribuição da riqueza. As mesmas leis estatísticas que governam as colisões aleatórias de átomos minúsculos, a progressão inelutável em direção à máxima entropia [5], garantem que o dinheiro seja distribuído de maneira muito desigual. Uma pequena minoria terá muito dinheiro e um grande número de pessoas terá muito pouco.
Por que surge essa distribuição? É fácil entender a essência dessa dinâmica: em cada transação só pode haver um vencedor e um perdedor. Pela força do acaso, algumas pessoas terão uma longa sequência de vitórias e acabarão com muito mais dinheiro que o resto.
2 O conceito de equilíbrio estatístico
O modelo de economia simples ilustra o conceito de equilíbrio estatístico. Com o passar do tempo, a distribuição da riqueza na economia converge para uma distribuição exponencial e permanece por lá. Mesmo que os atores econômicos individuais continuem realizando trocas de dinheiro e subindo ou descendo na escala da riqueza, a distribuição geral da riqueza na economia permanece constante. Algumas pessoas pobres podem ficar ricas, outras pessoas ricas podem ficar mais pobres, mas a situação geral permanece a mesma. Um pequeno número de pessoas acaba ficando com muito dinheiro.
Compare esse tipo de equilíbrio com o conceito de equilíbrio mais conhecido, de equilíbrio mecânico. Por exemplo, considere uma balança com 1 kg na bandeja esquerda e 1 kg na direita: os pesos se equilibram, todas as forças se igualam e os braços permanecem imóveis. O sistema está em equilíbrio mecânico e permanecerá assim até que seja aplicada alguma força externa. Um equilíbrio estatístico é um tipo diferente de equilíbrio. Ao contrário de um equilíbrio mecânico, no qual a configuração do sistema permanece estática, um sistema pode estar em equilíbrio estatístico, mesmo enquanto sua configuração muda continuamente. É a distribuição das probabilidades entre as possíveis configurações do sistema o que permanece constante ao longo do tempo. Por exemplo, se extraimos uma amostra da distribuição de dinheiro no modelo de economia simples por um período de tempo e então repetirmos esse experimento posteriormente, as duas distribuições terão alta probabilidade de serem quase idênticas, apesar do dinheiro mudar constantemente de mãos. Portanto, diferentemente de um equilíbrio mecânico, há sempre a possibilidade de que um sistema em equilíbrio estatístico se desvie espontaneamente do equilíbrio, mas a probabilidade de que o faça é pequena. Por exemplo, a probabilidade de que o modelo de economia simples retorne espontaneamente à sua distribuição de riqueza igualitária inicial é tão absurdamente pequena que pode ser considerada impossível.
O padrão das teorias econômicas que herdamos do século XX são modelos determinísticos, seguindo o caminho traçado pelos teóricos do século XIX que copiaram as ferramentas e os métodos das teorias mecânicas predominantes nas ciências físicas (Mirowski, 1989). A primeira formulação definitiva dessa abordagem está no pequeno livro de Debreu, A Teoria do Valor (Debreu, 1959), no qual uma economia de mercado é retratada como uma enorme calculadora determinística que computa um conjunto de trocas de mercado entre os atores econômicos, de maneira agradável a todos, dada uma relação inicial de bens. Neste modelo, o conceito de equilíbrio mecânico é empregado para a compreensão do significado dos fenômenos econômicos. Porém, diferentemente das configurações mecânicas da matéria, que às vezes de fato chegam até o estado de repouso, uma economia de mercado nunca o faz: ela é inerentemente um sistema dinâmico, com atores econômicos cuja agência perturba continuamente qualquer possibilidade de se alcançar um equilíbrio mecânico. Uma economia de mercado é muito mais como um saco de bolas de gude sendo chacoalhado vigorosamente do que como um conjunto de balanças em repouso.
O caso mais simples de equilíbrio estatístico analisado nas ciências físicas é o de um gás ideal. Um gás ideal consiste em milhões de partículas idênticas dentro de um recipiente perfeitamente isolado. Assume-se que o volume e a temperatura do gás sejam constantes. Cada partícula de gás se move continuamente dentro do compartimento, se chocando com as paredes e com outras partículas, mudando de direção e ganhando ou perdendo velocidade, dependendo das contingências locais que determinam os resultados de cada colisão. No nível micro, parece haver caos – mas apesar de todo o caos descoordenado, porém, todas as partículas estão conectadas umas às outras através do princípio da conservação de energia. Cada colisão conserva a energia, e portanto a energia total do sistema é constante. Assim, se uma partícula estiver viajando extraordinariamente rápido e tiver uma grande energia cinética, isso necessariamente implica que outras partículas devem se mover a uma velocidade mais lenta: é uma impossibilidade física que todas as partículas tenham a energia cinética mais alta no mesmo instante. Em outras palavras, existe um suprimento compartilhado de energia disponível que é distribuído entre as partículas de gás. Essa energia total é uma restrição em nível macro sobre a desordem no nível micro: nenhuma configuração possível do sistema – ou seja, nenhuma possível distribuição de energia cinética entre as partículas do gás – poderia violar essa restrição global.
A lei fundamental do equilíbrio na mecânica estatística é a lei de Boltzmann-Gibbs, que afirma que a distribuição das probabilidades da energia [10] é
onde T é a temperatura do gás ou a energia média por partícula. [6] Novamente, trata-se da distribuição exponencial – o que não surpreende, quando consideramos que o modelo de economia simples e o gás ideal são formalmente equivalentes:
| Modelo de Economia Simples | Gás ideal |
| Grande número de atores idênticos | Grande número de partículas idênticas |
| Cada ator possui a quantia em dinheiro mi | Cada partícula possui o nível de energia i |
| Dinheiro total M é constante | Energia total E é constante |
| As trocas conservam o dinheiro | As colisões conservam a energia |
| A economia entra em equilíbrio estatístico | O gás entra em equilíbrio estatístico |
| Distribuição de Boltzmann-Gibbs para a quantidade de dinheiro | Distribuição de Boltzmann-Gibbs para o nível de energia |
 |  |
| 1/λ é a riqueza média | 1/λ é a temperatura média |
3 A distribuição de máxima entropia
Na seção 1.4 [no livro] foi introduzida a segunda lei da termodinâmica, que afirma que a entropia total em um sistema fechado tende a aumentar. [5] O modelo de economia simples e o gás ideal são sistemas fechados. A segunda lei implica que a distribuição de equilíbrio, que já vimos que é a distribuição exponencial, deve ser a distribuição que possui a máxima entropia, dada a restrição geral sobre o dinheiro total para a economia (ou a energia total para o gás). Vamos verificar isso. Considere a seguinte medida de entropia [5] para o modelo de economia simples:
onde P(m) é a probabilidade de um ator escolhido aleatoriamente possuir 
[N.M.: neste artigo vamos assumir esta fórmula como simplesmente dada, já que o tema da entropia em sistemas fechados e a sua medida são discutidos em outros capítulos do livro. Ver a nota [5]. ]
Seja nm o número de atores que possuem
[N.M.: ou seja, o somatório ( 
e
[N.M.: ou seja, o somatório (
A probabilidade de um ator escolhido aleatoriamente possuir a quantidade de dinheiro
[N.M.: ou seja, essa probabilidade é igual ao números de atores (nm) que possuem
Se substituirmos nm = P (m) N nas duas equações acima [7], obteremos duas restrições sobre as probabilidades:
que é a restrição simples de que a soma de todas as probabilidades deve ser igual a um; e
que é a restrição de que as probabilidades devem estar em conformidade com a restrição da riqueza total.
O problema matemático é determinar uma fórmula para 
Na realidade, diferentemente do modelo de economia simples, existem muitos esquemas para a realocação de dinheiro – por exemplo, a redistribuição limitada de renda via impostos estatais. É um fato surpreendente, no entanto, que tais mecanismos não afetem a forma funcional geral da distribuição de riqueza. Os mercados parecem possuir uma tendência muito robusta para maximizar a entropia e para gerar distribuições de riqueza altamente desiguais e predominantemente exponenciais.
Revisaremos o tópico da desigualdade no Capítulo 13 [no livro], onde descobriremos que as distribuições completas de riqueza e de renda possuem entropia menor do que a distribuição exponencial. Portanto, novos fatores causais – ausentes nesse modelo simples de economia – estão em ação, impondo restrições adicionais sobre as probabilidades P(m). Isso implica que algum tipo de obra “demoníaca” [9] de redução de entropia está sendo realizado para “repartir” o dinheiro entre as diferentes classes econômicas.
4 Agentes aleatórios versus agentes racionais
Neste ponto, é possível levantar a objeção de que os atores econômicos são claramente intencionais e que, portanto, seria essencial modelar a racionalidade individual, mesmo quando consideramos fenômenos de nível macro, como as distribuições emergentes de riqueza e de renda. Por exemplo, as pessoas não trocam dinheiro de acordo com regras aleatórias e, dependendo dos valores envolvidos, geralmente elas pensam com muito cuidado sobre aquilo com que gastam. No entanto, essa objeção confunde epistemologia com ontologia, um quadro com a realidade. Um modelo aleatório não precisa implicar que a causalidade que ele representa seja aleatória, apenas que é intrinsecamente difícil de se modelar toda a causalidade de maneira perfeitamente detalhada. A aleatoriedade pretende representar todas as muitas e variadas decisões racionais (ou não) dos atores econômicos.
A premissa subjacente à abordagem baseada em atores racionais para a Economia é que os fenômenos no nível macro seriam redutíveis aos mecanismos da racionalidade individual e determinados por eles. Farjoun e Machover (1983) já há algum tempo observaram que a bem sucedida teoria física da Mecânica Estatística está em contradição direta com essa premissa. Por exemplo, a mecânica estatística clássica modela as moléculas de um gás como bolas de bilhar idealizadas, perfeitamente elásticas. É claro que isso é uma simplificação grosseira da estrutura de uma molécula e de como ela interage com outras moléculas. Ainda assim, a mecânica estatística é capaz de deduzir macro-fenômenos empiricamente válidos. Aleksandr Khinchin, que ajudou a transformar a mecânica estatística clássica em um tópico matematicamente rigoroso, colocou desta maneira:
As leis gerais da mecânica utilizadas na mecânica estatística são necessárias para quaisquer movimentos de partículas materiais, independentemente de quais sejam as forças causando tais movimentos. É a completa abstração da natureza dessas forças o que confere à mecânica estatística suas características específicas e o que contribui com toda a flexibilidade necessária para as suas deduções. […] [O] caráter específico dos sistemas estudados pela mecânica estatística consiste principalmente no enorme número de graus de liberdade que esses sistemas possuem. Metodologicamente, isso significa que o ponto de vista da mecânica estatística é determinado não pela natureza mecânica, mas pela estrutura de partículas da matéria. É quase como se o objetivo da mecânica estatística fosse observar até que ponto podem chegar as deduções feitas com base na estrutura atômica da matéria, independentemente da natureza desses átomos e das leis de sua interação.
O método de se abstrair as mecânicas da racionalidade individual e de, ao invés disso, enfatizar a natureza dos indivíduos como “partículas” é válido porque o número de graus de liberdade da realidade econômica é muito grande. Podemos representar a tomada de decisão individual de maneira altamente simplificada como uma seleção aleatória a partir de possibilidades restritas por princípios gerais em um nível macro, como a conservação do dinheiro. Nesse nível de abstração, a psicologia individual pode ser modelada como um ruído irrelevante.
No próximo capítulo [no livro] examinaremos em mais detalhes o modelo de economia simples e sua relação com as equações físicas da mecânica estatística.
Tradução: Everton Lourenço
Anexo 1 – A distribuição de Boltzmann–Gibbs
Plotagem da distribuição de probabilidades em escala log-log
Plotagem da distribuição de probabilidades em escala linear
A distribuição de Boltzmann-Gibbs caracteriza as energias das partículas em um sistema termodinâmico. Ela tem a forma geral 
Essa distribuição surge como consequência do fato de que em um sistema fechado de partículas a energia total deve ser conservada, mas as trocas aleatórias de energia entre essas partículas fazem com que a energia se espalhe pela população em um padrão específico. A probabilidade de uma partícula individual ganhar energia adicional sucessivamente a partir de uma sequência de trocas é bem baixa. Portanto, podemos esperar observar a maioria das partículas com baixa energia (o caso mais provável), mas um pequeno número com uma quantidade desproporcionalmente enorme de energia. O gráfico mostra que a probabilidade de uma partícula possuir [o nível de] energia mais alta (100) é muito baixa.
Dragulescu e Yakovenko (2002) argumentaram que, como o dinheiro é conservado na troca de mercadorias, a distribuição do dinheiro deve seguir uma forma funcional semelhante. Veremos no capítulo 11 [no livro] que a premissa da conservação do dinheiro só pode ser mantida em certa medida em uma economia capitalista com bancos modernos.
Notas
[1] Originalmente, “capítulo”. Trata-se do capítulo 7 do livro, “The probabilistic approach to economic variables” (“A Abordagem Probabilística Para as Variáveis Econômicas”). [N.M.]
[2] Em 1994, os artistas de vanguarda escoceses Bill Drummond e Jimmy Cauty queimaram um milhão de libras, ganhos com as vendas de seus discos pop, mas esses eventos têm baixa probabilidade.
[3] Você pode assistir a esse processo em tempo real na web; ver Wright (2008a).
[3b] N.M.: Seguem abaixo três prints de momentos diferentes de uma simulação desse modelo, conforme apresentado pelo autor no próprio link em que podemos rodar a simulação:
- Modelo de economia simples no estado inicial, com todo o dinheiro M distribuído igualmente entre todos os N atores (500, nesse exemplo):
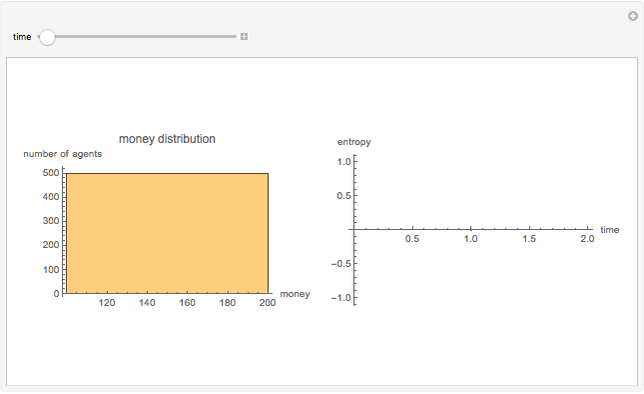
2. Com o modelo rodando a algum tempo, o dinheiro começa a ser distribuído de maneira bastante desigual entre os atores, conforme previsto, concentrando a maioria dos atores nos compartimentos representando quem possui quantidades mais baixas de dinheiro, e a medida da entropia do sistema (no sentido de desordem) cresce:
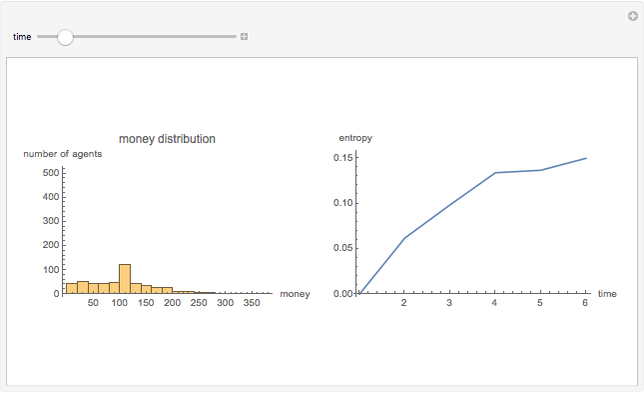
3. À partir de certo momento, o sistema entra em equilíbrio estatístico em torno da distribuição de Boltzmann-Gibbs da posse de dinheiro pelos atores no modelo (muito desigual, em torno de uma distribuição exponencial), e a entropia se estabiliza próxima de seu valor máximo:
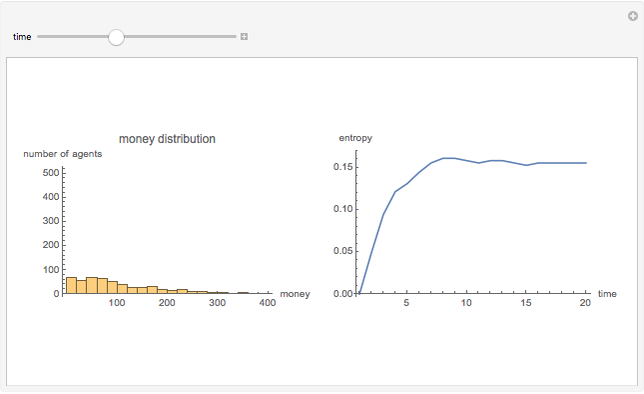
[4] Alguns estudos empíricos usam a renda durante um período de tempo como um proxy para a riqueza instantânea, mas os detalhes não importam aqui.
[5] Os conceitos de entropia, máxima entropia e entropia total para sistemas fechados (além do próprio conceito de “sistema fechado”) são trabalhados no livro em capítulos anteriores, incluindo a equação da entropia total para o sistema. Por enquanto, para o leitor não familiarizado, vale a pena trabalhar com essas equações como dadas. Mais à frente pretendo traduzir aqui em O Minhocário alguns trechos de outros capítulos para tentar facilitar a compreensão dessas ideias, e aí atualizarei este artigo para incluir os links para essas explicações. [N.M.]
[6] O que pode ser reescrito como
[7] [N.M.] No caso, apenas foi feita uma manipulação algébrica simples sobre a equação, “jogando para o outro lado” o N para isolar nm, seguindo essas etapas:
- e invertendo a ordem:
Logo em seguida, com base nisso, o valor de nm foi substituído por P (m) N nas 2 equações apresentadas logo acima no trecho do texto, com as seguintes etapas:
Equação 1:
Equação 2:
Por isso as duas equações que são apresentadas logo em seguida no texto. [N.M.]
[8] O leitor interessado deve consultar Kapur (1989) e Kapur e Kesavan (1992).
[9] Aqui neste artigo essas referências a “demônio econômico” ou “obra demoníaca” podem parecer um pouco soltas e sem sentido, mas elas estão retomando um famoso exemplo já discutido em capítulos anteriores em que Maxwell imagina um demônio trabalhando contra a tendência da entropia em um sistema fechado. Como já indiquei na nota [5], esse é mais um caso em que as coisas ficarão mais nítidas quando publicarmos em outra postagem a tradução de trechos de capítulos anteriores do livro, discutindo o conceito de entropia. [N.M.]
[10] [N.M.] Neste artigo foram usadas 4 diferentes equações para representar a probabilidade de um determinado ator (ou uma determinada partícula) estar em um determinado ponto da distribuição de Boltzmann-Gibbs. Essas diferentes equações podem contribuir para uma certa confusão, principalmente para quem tem um pouco mais de dificuldade nessa área. No entanto, todas essas versões são formas equivalentes de expressar a mesma probabilidade dentro da mesma distribuição, variando apenas a notação das equações (seja por costume, ou seja pela diferença de contexto). Portanto, na prática, todas as equações abaixo podem ser vistas como a mesma equação, com o mesmo significado geral. A compreensão das razões matemáticas para que essa seja a forma da distribuição de Boltzmann-Gibbs não é relevante para os propósitos deste artigo, bastando na verdade que o leitor compreenda a dinâmica geral da própria distribuição – caracterizada por uma grande desigualdade, como explicado no anexo 1 – e como ela é característica do equilíbrio estatístico de sistemas com alto grau de liberdade dos seus elementos constituintes (atores ou partículas) (e o leitor mais interessado nessas razões matemáticas pode buscar referências no campo da Termodinâmica para se aprofundar nesse tópico, inclusive nas próprias referências no final do artigo). Abaixo apresento as 4 formas da equação de distribuição de Boltzmann-Gibbs utilizadas no artigo, explicando as diferenças de notação entre elas e como ler cada uma delas. A primeira a aparecer no artigo é a versão número quatro da equação (a última na lista abaixo), já representando a distribuição das probabilidades no modelo de economia simples.
-
A versão um pouco mais extensa da equação, utilizada no contexto da Termodinâmica para modelar as probabilidades de distribuição das partículas em um gás ideal (como explicado na sessão 2, sobre equilíbrio estatístico):
que também poderia ser reescrita como
ou ainda como
para destacar a repetição de
Podemos ler essa equação da seguinte maneira: a probabilidade (
) de uma determinada partícula no gás ideal possuir um determinado nível de energia (
) , multiplicado pela constante de euler (
, ou seja 2.7182… ) elevada a menos o resultado da divisão entre o nível de energia (
-
onde λ = 1/T.
A segunda versão da equação também é utilizada no contexto da Termodinâmica para modelar as probabilidades de distribuição das partículas em um gás ideal (como explicado na sessão 2, sobre equilíbrio estatístico). A única diferença desta versão em relação à anterior é que 1/T, que aparece duas vezes na equação anterior, é substituída pela variável λ para simplificar a expressão geral da equação.
Portanto, podemos ler essa equação da seguinte maneira:a probabilidade (
, multiplicada pela constante de euler (
, ou seja, 1 dividido pela temperatura total ou média de energia do gás como um todo (
-
A terceira versão da equação também é utilizada no contexto da Termodinâmica para modelar as probabilidades de distribuição das partículas em um gás ideal (como explicado na sessão 2, sobre equilíbrio estatístico). Esta versão da equação troca o símbolo de proporcionalidade ( ∝ ) pela igualdade seguida por uma constante
que multiplica o resto da equação (ou seja, algum número real que, na prática, não fará diferença para se compreender a dinâmica apresentada). Além disso, nessa versão, como
não deixa de também representar uma outra constante (envolvendo temperatura total ou média de energia do gás como um todo –
), essa parte da equação é suprimida como parte da constante
Portanto, podemos ler essa equação da seguinte maneira: a probabilidade (
-
Esta versão da equação, diferente das outras três, aparece no contexto do modelo de economia simples, como discutido nas sessões sobre “uma economia de trocas simples” e sobre “o conceito de equilíbrio estatístico”. Esta versão é semelhante à versão 2 indicada acima, também usando a substituição de 1/M pela variável λ para simplificar a expressão geral da equação (mas dessa vez o autor deixou implícito que λ = 1/M, não declarou diretamente). A única diferença é que, como representa a versão dessa equação para o modelo de economia simples estudado nesse artigo, ao invés da versão original usada para o estudo de um gás ideal, esta versão da equação troca o parâmetro (significando o nível de energia carregado pela partícula de gás no modelo de gás ideal) por
Portanto, podemos ler essa equação da seguinte maneira: a probabilidade (
, ou seja, 1 dividido pela quantidade total de dinheiro no modelo de economia simples (
). [N.M.]
Referências Bibliográficas
Debreu, G. (1959) “Theory of Value: An Axiomatic Analysis of Economic Equilibrium” (“Teoria do Valor: Uma Análise Axiomática do Equilíbrio Econômico“), New Haven: Yale University Press.
Dragulescu, A. A. (2002) “Applications of Physics to Economics and Finance: Money, Income, Wealth, and the Stock Market” (“Aplicações da Física para a Economia e as Finanças: Dinheiro, Renda, Riqueza e Mercado de Ações“). Ph.D. thesis, Department of Physics, University of Marylan .
Dragulescu, A. A. e V. M. Yakovenko (2000) “Statistical mechanics of money” (“Mecânica Estatística do Dinheiro“), The European Physical Journal B 17: 723–729.
Dragulescu, A. A. e V. M. Yakovenko (2002) “Statistical mechanics of money, income and wealth: a short survey” (“Mecânica Estatística do Dinheiro, Renda e Riqueza: uma Breve Revisão“).
Farjoun, E. e M. Machover (1983) “Laws of Chaos, a Probabilistic Approach to Political Economy” (“Leis do Caos: Uma Abordagem Probabilística para a Economia Política“), London: Verso.
Kapur, J. N. (1989) “Maximum Entropy Models in Science and Engineering” (“Modelos de Entropia Máxima nas Ciências e Engenharia“), Wiley Eastern.
Kapur, J. N. e H. K. Kesavan (1992) “Entropy Optimization Principles with Applications” (“Princípios e Aplicações de Otimização de Entropia“), Academic Press.
Khinchin, A. I. (1949) “Mathematical Foundations of Statistical Mechanics” (“Fundamentos Matemáticos da Mecânica Estatística“), New York: Dover
Mirowski, P. (1989) “More Heat Than Light: Economics as Social Physics, Physics as Nature’s Economics” (“Mais Calor Que Luz: Economia como Física Social, Física como Economia Natural“), Cambridge: Cambridge University Press.
Wright, I. (2008a) “Statistical mechanics of money” (“Mecânica Estatística do Dinheiro“) . Wolfram Demonstrations Project.
O Minhocário 
Pingback: Trabalhar menos e viver melhor – DMT – Democracia e Mundo do Trabalho em Debate